
What are instructional routines?
"Instructional routines are specific and repeatable designs for learning that support both the teacher and students in the classroom... enabling all students to engage more fully in learning opportunities while building crucial mathematical thinking habits." Kelemanik, Lucenta, & Creighton (2016)
The Instructional Routines on this page are accessible and challenging to all students, can be approached in multiple ways using different types of sense-making strategies, promote understanding through discussion, make student thinking visible, make math visual and encourage practice of mental math
Instructional Routines:
This growing collection features resources and support for bringing the following instructional routines into your classroom:

Are there any additional instructional routines you think should be included on this page? Click HERE to let us know!
|
1) Notice/WonderStart problem-solving without the problem. Leave off the question, give students a math situation, graph or image and ask them: "What do you notice? What do you wonder?"
| | |
2) Dot TalksDot talks are a great way to show how visual math can be and how many different ways there can be to look even at a simple image. They take about 10-12 minutes to do. In a dot talk, a teacher shows an image of dots for a couple of seconds and then asks students how many they saw. (The important thing is that students are not counting the dots one by one.) Then each student describes their way of seeing the dots. The teacher visually records each student's way of seeing and creates (or asks students to create) an expression representing the student's way of seeing. For the dot talk below, ANN member Patricia Helmuth, NY recorded different ways of seeing by making multiple copies of the image of the dots. 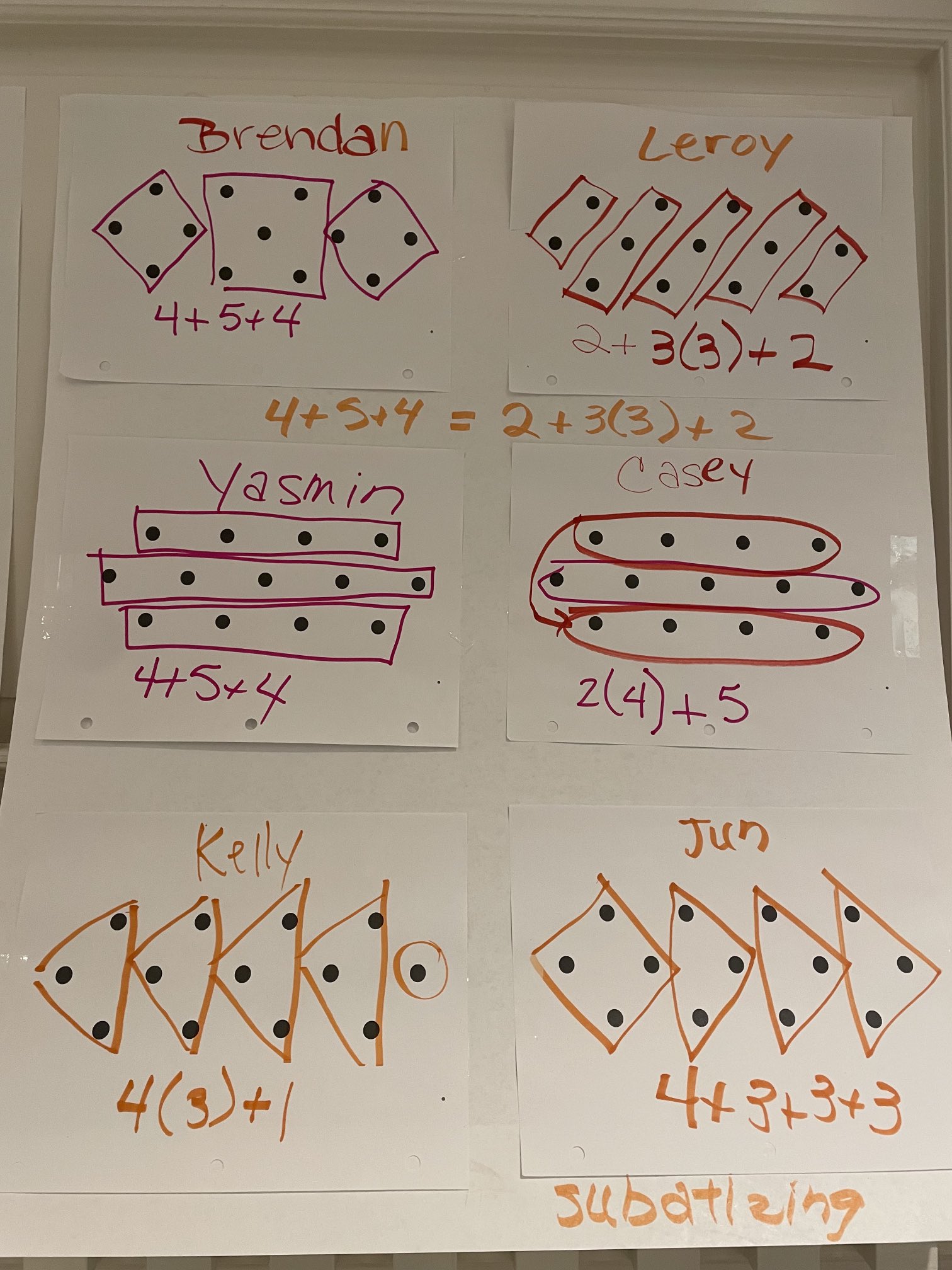
| |
- When Steve Wyborney does dot talks with his students, he does one as described above. Then he gives students another set of dots, but the second time, each student receives a handout with 18 copies of the same collection of dots. Their task is to notice as many ways of seeing the dots as they can, record it similar to how Patricia did and write an expression for each way of seeing. To learn more, read his post, Provide Massive Space to Notice. Also check out 180 Opportunities to Notice - 10 pages of dot patterns he created that you can download and use with your students.
- Cindy Whitehead created a Desmos activity called Crazy Eights, where students need to match equations to a dot pattern, create an equations that match dots patterns and create dot patterns that match equations.
|
| |
There are 22 dots total. How many are under each Splat? 

|
4) Fraction TalksA Fraction Talk is a discussion-rich routine that invites multiple ways of identifying fractions. They are similar to number talks, but instead of drawing out strategies through mental calculations, students evaluate images like this one and asking questions like, "What fraction of this figure is yellow?" Nat Banting created the Fraction Talks website, which has a huge collection of images to inspire discussion and exploration, as well as suggestions for using this routine in your class. Check out his 12 Days of Fraction Talks. MATH FOR LOVE has some great Fraction Talk images using pattern blocks. To watch a video of a fraction talk in action in an adult eduction class, visit SABES Instructional Routine: Fraction Talks
| |
What fraction of this figure is yellow? How do you know?
| |
What fraction of this shape is blue? How do you know?
|
5) Number Talks / How many ways?
A Number Talk takes about 10-15 minutes and help students develop their number sense and teach them that they have mathematical ideas worth listening to and that they can make sense of calculations in their own ways. Especially for adult education students, many of whom received a fragile understanding of number and calculations from their prior education. The basic routine is students do a mental calculation without using paper. Students explain their thinking and teachers create visual representations of that thinking.
Here are some resources to start using Number Talks in your class.
Pam Harris facilitates a weekly slow chat on Twitter called #MathStratChat. Her collection of computation problems are thoughtfully designed and make for rich number talks. and have the added bonus of multiple approaches.
MATH FOR LOVE has a nice collection of resources for using number talks.
| |

Berkeley Everett created adaptable slides so teachers can make customized number talk images using fruit, nuts, and pastries. Custom Number Talk Images Kristen Acosta has a collection of Number Talk Images for inspiring great math discussions.
|
6) Number Strings/Problem StringsNumber strings, also called problem strings, refer to a related series of mental math problems that are designed to help students notice relationships and develop explicit reasoning strategies. Number Strings is a website for math educators to find number strings, share number strings, get feedback, and interact with other teachers using number strings with learners. It is a growing resource, and currently has addition strings, subtraction strings, multiplication strings, division strings, rational number strings, and algebra strings.
Pam Harris has created an introduction to problem strings that include (1) videos showing the string in action with students, (2) a written description of the mathematics, (3) explanation of the teacher moves, and an annotated transcript of the video. These can all be found at her website: Math Is Figureoutable - Problem Strings Harris has a free, 2-page introduction called What is a Problem String? available to download. She also created a document titled The Most Important Numeracy Strategies, also available for free download.
| | |
7) Test Talks
A Test Talk is an instructional routine developed by Aren Lew designed to (1) help students apply and extend their learning in the context of standardized test questions, (2) Solidify learning and act as a formative assessment, (3) Empower students to think flexibly and creatively in test situations, and (4) Build students’ capacity to make sense of problems and persevere in solving them
Test Talks help create and nurture a classroom culture that values flexible thinking and conceptual understanding and that explicitly prepares students to apply their learning in the context of standardized tests.
| | |
8) Visual Patterns are a great way to utilize patterns to encourage making use of structure in problem-solving. Students make observations and build on those observations to generalizations.
Visual Patterns is a collection of hundreds of visual patterns gathered by Fawn Nguyen. There are patterns that can be used to explore linear function, quadratic functions, cubic functions,
For some ideas about how to use visual patterns with adult students, including handouts and a lesson plan, read Developing Algebraic Reasoning Through Visual Patterns Mathigon has a visual pattern tool that can help make students' thinking visible to classmates and teachers.
| |

Here are the first 3 steps of a visual pattern. 
What comes next? 
|
9) Estimation 180Estimation 180 is a collection of engaging photos and short videos developed by Andrew Stadel. The visuals are used as estimation challenges (like the one to the right) that help students develop their number sense through reasoning, multiple estimation strategies, explaining their ideas, connecting to different math content, and reflecting on the process. To learn more about using Estimation 180 with adult education students:
| |
How long is I Got You (I Feel Good)? 
|
10) Which One Doesn't Belong?
With this instructional routine, teachers present four of something (like the 4 numbers to the right) and ask students to come up with reasons why each doesn't belong.
The website Which One Doesn't Belong? (WODB) is a collection of Numbers, Shapes, and Graphs to explore, curated by Mary Bourassa, inspired by the book Which One Doesn't Belong by Christopher Danielson. Start there or create your own!
You can find ideas on how to use WODB with adult students: Learning Through Classification
Use this WODB Template in Desmos to create your own interactive Which One Doesn't Belong.
For a variation of the WODB routine, try How Does It Belong? on Desmos.
| |
What makes each of these numbers different from the other three? 

|
There is a WODB Generator on Polypad that uses prime factor circles, fraction circles, dice, dots, equations, rectangular prisms, and more. Just click on the Generate! button to produce a new WODB.

With fraction circles, you can label the pieces as fractions, decimals, percentages, or not at all (as seen above). You can also remove the unit fraction dividers (the white lines).

| |

With the factor circles, you can label the products (as seen above), and/or the prime factors around the circle. 
|
11) Slow Reveal Graphs
Slow Reveal Graphs refers to a process for using graphs with students that promotes sense-making. You start with a graph and peel back the layers until you have a numberless graph that every student can make observations about. Then you add back the layers, step by step, encouraging students to make sense of the graph and engage with the story of the graph.
Slow Reveal Graphs is a collection of slow reveal graph sequences organized by type of graph as well as by context. The site is curated by Jenna Laib.
The CUNY Adult Literacy Program has a growing collection of Slow Reveal Graphs in SS and Science.
In this brilliant article from the Math Practitioner (Summer 2022 issue), Tim Berrigan, NY explains how he uses slow reveal graphs in his classroom and why the routine is so effective - Slow Reveal Graphs: A Powerful Instructional Routine
| | |
12) Numberless Word ProblemsMany students in adult education struggle with word problems. Because of their prior educational experiences often emphasized memorization and tricks over sense-making, they sometimes throw numbers together without thinking about the mathematics in the situation. Similar to slow reveal graphs, numberless word problems involve removing the layers of a word problem and then adding the layers back, one at a time, giving students space and time for sense-making and discussion. Brian Bushart's website, NUMBERLESS WORD PROBLEMS has ready-to-use and ready-to-customize numberless word problems, as well as suggestions for getting started using this instructional routine with your students. The CUNY Adult Literacy Program has started a collection of Numberless Word Problems to use with adult education students.
| |
Here is a sample sequence from Brian Blockhart's site: - A baker is packaging some cupcakes to sell at her bakery. She fills some boxes with all of the cupcakes.
- A baker is packaging 30 cupcakes to sell at her bakery. She fills some boxes with all of the cupcakes.
- A baker is packaging 30 cupcakes to sell at her bakery. She fills 5 boxes with all of the cupcakes.
- A baker is packaging 30 cupcakes to sell at her bakery. She fills 5 boxes with all of the cupcakes. If she puts the same number of cupcakes in each box, how many cupcakes are in one box?
|
13) Three-Act Math Tasks
The 3-Act Math task routine was developed by Dan Meyer.
- Act 1 is the hook. It is visual - often a photograph or a brief video - accessible to all and has no numbers. The goal of Act 1 is to inspire curiosity and student-generated questions. The video to the right is Act 1 of a Three-Act math task called The Taco Cart.
- Act 2 is where students get involved in the formulation of the problem. They decide what information is needed and what matters.
- Act 3 is the big reveal – usually a photo or a brief video clip. Then students talk about their initial guesses, their process, their results and the reveal.
You can create your own 3-acts, but to help you get started, visit Dan Meyer's Collection of 3-Act Math Tasks
Read more about using Three-Act Math Tasks with adult learners - Inspiring Student Curiosity (or What's real about real-world math?)
| |
Watch the video below about Dan & Ben (29 seconds) - What question(s) do you have? What do you think will happen?
- What information would you need to answer those questions?
After you answer the questions above, check out Acts 2 and 3 (and the extensions) here: Taco Cart - Three-Act Math Task
|
Kristen Acosta, a K-8 Math Coach in California has created several dozen Three-Act math tasks for grade K-6 standards. You can access them all for free at Kristen Acosta - Three Acts
14) Always, Sometimes, NeverThe basic structure of the Always, Sometimes, Never routine is, students are given a series of mathematical statements to sort into one of three categories: "always true," "sometimes true," or "never true." Students, usually in groups, have to defend their answers and come up with examples and counterexamples. A good way to get started with Always, Sometimes, Never is this brief blog post by Fawn Nguyen describing using the routine with her students. The image here shows the work of some of her students. In her post, Fawn shares another collection of statements developed by Swan and Ridgway. Consider a few statements that Fawn shared with her students. Which column would you place them in? - Max gets a pay raise of 30%. Jim gets a pay raise of 25%. So Max gets the bigger pay raise.
- When you cut a piece off a shape, you reduce its area and perimeter
- The square root of a number is less than the number.
- 2(3 + s) = 6 + 2s
| | |
15) Solve Me MobilesSolve Me Mobiles allows students to develop algebraic thinking through balance puzzles like the one to the right. The site offers a collection of puzzles and allows teachers (or students) to create their own.
| | |
16) Clothesline Math
Clotheslines are interactive number lines. Students place (and move) cards on a clothesline where they think the number belongs. It is a great activity to show proportional reasoning, precision, equivalency between numbers, and magnitude. The clothesline draws out student sense-making around relationships between numbers. It can be used across a range of math content, from building students’ number sense to algebra. Read What is Clothesline Math? from the Summer 2024 issue of the Math Practitioner. Kristen Acosta's clothesline math cards can be used to explore topics like fractions, decimals, percents, integers, money and expressions. Patricia Helmuth's Numeracy Adventure Day materials has a clothesline activity with many number representations. In this blogpost - The Intersection of Fraction Talks & Clothesline Math: Formative Assessment - Jenna Laib writes about a clothesline math activity with fractions. Her description includes her planning, photos of students work, and the connections she made during the class discussion.
| | |
Theresa Wills' created a virtual template for Clothesline Math using Google Slides. Teresa's take on Clothesline Math is give students a range and let them create the number they want to place on the line (as opposed to placing a number they are given). For example, a teacher could set the range of the numberline between 3 and 5. Then ask students to write a number between 3 and 5 on a card and add it to the line. You can encourage students to be creative and try to write a number that they think other students won't come up with. Another fun way to have students create the number is to give them an image from the FractionTalks website (see below), ask them to color in whatever portion they want, and then place the fraction represented on the clothesline.
17) Can You See It? I learned this routine from Dee Crescitelli. It is a great way to strengthen connections between visual representations and quantities. It allows you to assess students in a puzzle-like atmosphere that lends itself to building a culture of collective knowledge building. It is a simple set up. Provide a visual like the one to the right and ask if folks can see the quantities in the image. Try it for yourself. Can you find all of those quantities in those colored circles?
| | |
18) What math do you see?So many students have internalized an invisible barrier at the door to our math class, and all the math they do in their lives everyday gets devalued and checked at the door. If pressed, students will say most real-world math happens while shopping. Giving students an image and asking them to talk about the math they see is a great way to open up our ideas of what math is, where it happens, and why it is important. The question gives an opportunity for students to value the math they do and see in their lives and in their communities. The images here are just a few examples to get you started. We'd love to collect and share any images you use with your students! Send yours to mark.trushkowsky@cuny.edu or post them on Twitter using the hashtag #ANNMath. The Multiplicity Lab's Image of the Week (and their extensive archive) is full of images you can use to pose this question.
| | |
19) SAME or DIFFERENT?Similar to Notice/Wonder, Same or Different is a simple pair of questions to draw out student observations and mathematical argument.
Same or Different is a good introduction to this routine created by Brian Bushart. It has a collection of images and brief videos that teachers can use, but don't feel limited to what is there!
| |
What's the same? What's different? 
|
20) WOULD YOU RATHER?If you're looking for ways to engage students in math-based conversations, and having students use math to justify their ideas, check out the collection at Would You Rather Math. Connie Rivera, CT recommends this instructional routine because her students, "like being right by justifying their answer - even when it's different from someone else's choice."
| | |
21) Unit Chats For unit chats, teachers share an image with different kinds of objects to count, arranged in arrays or some other structure and ask students a simple question - “How many?”. Give students some time to see how many of which objects they see. Then after they have had 20 - 60 seconds to look, ask students what they see. As they share, open the floor for students to explain they different ways of counting what they saw and the different things they saw to count in the image. You can find a great introduction to unit chats, along with some compelling images at the Math for Love UNIT CHAT page.
| |
How many? 
|
22) Convince me that... "Convince me that..." is an easy to implement instructional routine that can be used with any math content. The routine draws out student visualizations and lots of language in a way that shifts the goals from finding solutions to communicating ideas. The basic structure is you find a word problem or problem, remove the question, give students the answer and then ask them to convince you that it's true. Here's a collection of over 100 examples of "Convince me that..." prompts, or you can create your own.
| | |
23) Push & Support CardsPush and Support cards are tools that allow teachers to dial up and dial down problems, keeping every student in a mixed-level math class engaged in high-cognitive level math tasks. Push and Support Cards: A Bridge to Advanced Math for a Mixed Level Adult Education Class is a guide written by Patricia Helmuth for using Push and Support cards with adult students. It explains how to use them, how to write your own, and has seven tasks with Push and Support cards already written to get you started.
| | |
24) Wrong Answers OnlyWrong Answers Only was developed by Zuzka Blasi, an adult education instructor in Massachusetts.
For this routine, present your students with a problem. Their task is to come up with an incorrect answer and to share their rationale for how they know the answer is incorrect.
Read more about how Zuzka uses this routine at the TERC Adult Numeracy Center blog post, Wrong Answers Only. Visit Instructional Routine: Wrong Answers Only (SABES) for a video of this routine in action and a Wrong Answers Only Starter Kit which includes sample prompts and sample wrong answers.
| | |
25) My Favorite No
My Favorite No is a great assessment activity that turns students’ mistakes into collective opportunities for learning. It can be done with any math topic or content. It takes very little time, so teachers can do it often and weave it into the daily routine of their class. This 6 min video provides an overview of the routine. For some ideas about how to use it with adult students, read My Favorite No: A Great Way to Celebrate Student Mistakes
| | |
26) Clarify, Critique, CorrectClarify, Critique, Correct is a math language routine where teachers give students a piece of mathematical writing (that is not their own) to analyze, reflect on, and develop. The intent is to prompt student reflection with an incorrect, incomplete, or ambiguous written argument or explanation, and for students to improve upon the written work by correcting errors and clarifying meaning. We learned about Clarify, Critique, Correct from Illustrative Math's collection of Math Language Routines.
| |
The goal of the routine is for students to discuss and understand why the mistake happened (more than just having them correct mistakes). For example, you might give students a fictional student statement like: 
And ask them to discuss in pairs/groups: Clarify: Why do you think this student wrote this?
Critique: What changes do you suggest? Why?
Correct: Improve the response.
|
27) Information GapDuring an Information Gap routine, students conduct a dialog in a specific way. One partner gets a Problem Card with a math question that doesn’t have enough information, and the other partner gets a Data Card with information relevant to the problem card. Students ask each other questions like “What information do you need?” and are expected to explain what they will do with the information. We learned about Info Gap from Illustrative Math's collection of Math Language Routines. Info Gap cards can be found throughout their free curriculum. Read a teacher describe why she likes the routine Info Gap Cards: The Hidden Gem.
| | |
Here's an example of what a Problem Card and a Data Card might look like:
| | |
28) Going on a Number Picnic Going on a Number Picnic is a math variation of a classic game "Going on a picnic." In the original version of the game, a player comes up with a rule in their head (ex. you can only bring things that have the letter L in them) and then says something like, "I'm going on a picnic and I'm bringing lettuce, lemons, and chanterelles but I'm not bringing mushrooms, spinach, or sandwiches." Then the other platers need to try to guess the rule by asking if they can bring certain items to the picnic. Can I bring apples? - Yes! Can I bring pears? - No!
| |
The number picnic version was developed by Carol Cashion, an adult education teacher in NYC. In Carol's version, you come up with a group/category of numbers (ex Multiples of 6) and say something like, "I'm going on a number picnic and I'm bringing 36, 48, and 54 but I'm not bringing 27, 33, or 63." Then students try to figure out the rule by asking if they can bring certain numbers to the picnic. Can I bring 66? - Yes! Can I bring 34? No!
There are all kinds of rules you can use for Going on a math picnic - you can make them as challenging or accessible as you like. For example, the rule could be: perfect squares, equivalent fractions, prime numbers, factors of 72, numbers who digits add up to 8, etc
It can help make two columns on the board (or a sheet of paper) - Yes and No to keep track of the guesses.
You can use Going on a Number Picnic to introduce a topic and you can also use it to review a topic. Once you've done it a few times together as a class, it's also fun to have students come up with their own rules and play in pairs.
|
29) Menu Math
Menu Math is an instructional routine developed by Nat Banting. A Menu Math task is a collection of 6-10 constraints that appear as an unordered list. For each task, there is a type of mathematical object that needs to be designed to satisfy these constraints. That object could be a certain type of function, an expression, a shape, a number, etc. Each constraint must be satisfied at least once, and students try to complete this goal using as few mathematical objects as possible. The structure provides a low entry point (teachers might ask students to design objects that satisfy one or two constraints), and a high ceiling (as students analyze which constraints pair well together and which cannot pair together).
| | |
30) Number of the Day
The basic routine of Number of the Day is simple: Give the students a number to consider each day. Students think of different ways to make that number. As you develop different number concepts in class, encourage your students to incorporate these concepts into the different ways they develop the number. 

| | |
31) Number Boxes This routine is a simple and flexible game that allows you to practice any arithmetic topic. It comes to us from Berkeley Everett, by way of ANN member Connie Rivera, CT. The game starts with an arrangement of blank lines or "number boxes" like the examples in the chart below. Players take turns rolling a dice. Both players must place the number rolled in their arrangement, though players do not have to put the number in the same place. Play continues until all of the blanks/boxes have been filled. Players determine which player is closer to the target and who wins. Here's an example of what a finished game might look like, courtesy of Berkeley Everett:

| |
Also check out:
Notice the two blanks written in the corner of each game card (36 on the left and 52 on the right)? During each game, players are allowed to discard up to two numbers, as long as they have a discard spot remaining.
|
34) If I knew... then I could This routine was suggested by Connie Rivera, CT. It comes from Advancing Equity and Strengthening Teaching through Elementary Mathematical Modeling. The goal of the routine is to help students identify quantities in a modeling situation. The basic structure of the routine is to present students with an image - like the one seen here - and give them the prompts "If I knew... then I could..." The folks from Advancing Equity and Strengthening Teaching through Elementary Mathematical Modeling created Supports for If I Knew... Then I Could... including images, editable sample slides, scaffolding options, and variations.
| | |
35) Look - Think - Talk
The Look- Think - Talk routine is straight-forward.
- Look: Show students an intriguing image and pose a mathematical question.
- Think: Give students a chance to think
- Talk: Engage students in discussion about the image and questions.
Our job is to open up space to explore big ideas in mathematics and to take advantage of the multiple ways students see and think. Create a space for their voices. Get them excited!

| |
Teachers' Guide for Getting Started (from the Multiplicity Lab out of Northwestern)
Search Collection of Look-Think-Talk Activities - Teachers can search the collection by one of 16 BIG IDEAS in math (i.e. "attending to and using structure," "composing and decomposing number," "equal means same," "relating part and whole," etc.). Handouts are available in English, Spanish, and Portuguese.
Seven Questions for Look-Think-Talk activities - Each activity uses one of the following 7 questions to frame what students are looking for, how they think about, and what they talk about. Teachers can search the collection by question. The seven questions are:
- How many?
- About how many?
- Which is more?
- What do you notice? What do you wonder?
- What patterns do you see?
- What's missing?
- How could you organize?
You may recognize some of the questions as instructional routines described on this page. Look-Think-Talk is another way to frame them with your students. There are brief videos available that explore the mathematical importance of each question.
|
36) Off You Go
In the Off You Go routine, the class focuses on a single concept – such as rectangles, patterns, the number 100, or half – and then students explore the environment to look for new ways that concept lives in the world. Students bring their diverse examples back for comparison and discussion, stretching their own notions of what the concept can (and cannot) look like. Think of this as a conceptual scavenger hunt. Students can do this as a full lesson searching your classroom or school, or try this as rich homework, where students look at home for a concept and you begin the next day’s lesson with sharing and discussion. The routine has three steps: 
| | |
Math educator Theresa Wills has created a collection of Google Slide templates that can be used to use many of the routines described on this page for remote intruction. Remote Instructional Routines

For suggestions on how to run many of these instructional routines virtually, check out Theresa Willis' Google Slide templates and videos
|

.jpeg)
.jpeg)

